Batch 3 - Class 146 - Induction Game of Patterns
Preclass Exercise:
- Gossip Problem: What if your goal, rather than minimizing the total number of conversations, is to minimize the maximum number of conversations that any one person has to participate in? Then how do you do it, how many total conversations does it take, and what is the maximum for one person?
- Breaking a Dollar:
- What if each arrangement (permutation) of the coins was counted differently? What would you have to change to produce the other answer
- Let students think about how to account for all permutations
- If they are unable to think through, help them get to a conclusion that we can "reduce" the problem just by looking at what the first coin is
- Help them arrive at equivalent formulae, and work through some entries on the board
- Instructor Notes: Help them organize it on an Excel sheet
- Wow! the answers here, with up to quarters, goes to 9+ Trillion!
Attendance: Smiti, Muskaan, Tishyaa, Anshi, Siddhant, Arnav, Anishka, Liza, Arjun
Class Notes:
Game of Patterns
(Mathematical Circus - Chapter 4)
Game of Patterns is an inductive game (Induction means going from specific to generalization) on a 6x6 grid. There is a designer, designs the nature, who puts a pattern with four symbols on the 6x6 grid. Example patterns below:
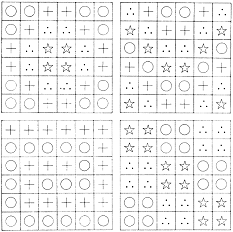
Other players have empty 6x6 grids. They can mark any number of squares with a small diagonal line in corner, and "ask" the designer about the symbol in those cells. They can do so any number of times, in no particular order. At any stage then, they can guess the symbols in all other cells, and give it to the designer for verification. This is like trying to figure out the order of nature. Finally, the scoring is as follows:
- Each person gets a score +1 for each correct guess, and -1 for each incorrect guess. The guesser may also drop out at any point, with zero score.
- The designer gets points basis the best and worst score of all guessers. The designer's points are (points of best guesser - points of worst guesser). Further, for each guesser who has dropped out, the designer loses 5 points for the first one, 10 for the second one and so on.
The above scheme ensures that the pattern should be such that some guesser can do very well at it, and someone else may do very poorly at it, but without dropping out.
Notion of strong conjecture - something that is easy to falsify, such as "all cells have stars". Weakest conjecture, hard to falsify, such as "any cell can have any symbol".
Let kids play the game and explore what kind of patterns work well. Rotate the role of Designer by throw of dice.
Homework:
- Five school girls were weighed in pairs and found to be 129, 125, 124, 123, 122, 121, 120, 118, 116 and 114 pounds. How much do they weight individually?
- Answer: 56, 58, 60, 64, 65. Reasoning below
- All girls must weight different, otherwise there would be repetition in pair weights. Let weights be a>b>c>d>e. Then largest weight must be a+b, then a+c. Lightest must be e+d, and then e+c. Sum of all the pair wise weights is 4(a+b+c+d+e) = 1212, and hence (a+b+c+d+e) = 303. Now c = (a+b+c+d+e)- (a+b) - (d+e) = 1212 - 129 - 114 = 60. a+c = 125, and hence a = 65, and a+b = 129, so b = 64. Similarly the rest.
References:
Mathematical Circus, Martin Gardner